Тест Chi Square в Excel - Как да направя Тест Chi Square с пример

Тест Chi-Square с Excel

Тестът Chi-Square в Excel е най-често използваният непараметричен тест, използван за сравняване на две или повече променливи за произволно избрани данни. Това е вид тест, който се използва, за да се установи връзката между две или повече променливи, това се използва в статистиката, която е известна също като Chi-Square P-стойност, в Excel нямаме вградена функция, но можем да използваме формули за извършване на хи-квадрат тест в Excel с помощта на математическата формула за тест с хи-квадрат.

Видове

1. Тест Chi-Square за доброта на прилягане
2. Тест Chi-Square за независимост на две променливи.

# 1 - Тест Chi-Square за добро състояние

Използва се за възприемане на близостта на извадка, която отговаря на населението. Символът на теста Chi-Square е (2). Това е сумата от всички ( Наблюдаван брой - Очакван брой) ² / Очакван брой.

• Където k-1 степени на свобода или DF.
• Където Oi е наблюдаваната честота, k е категория, а Ei е очакваната честота.

Забележка: - Доброто съответствие на статистическия модел се отнася до разбирането на това колко добре данните от пробите отговарят на набор от наблюдения.

Използва

• Кредитоспособността на кредитополучателите въз основа на техните възрастови групи и лични заеми
• Връзката между представянето на търговците и полученото обучение
• Възвръщаемост на единични акции и на акции от сектор като фармацевтичния или банковия сектор
• Категория на зрителите и въздействието на телевизионна кампания.

# 2 - Тест Chi-Square за независимост на две променливи

Използва се за проверка дали променливите са автономни една от друга или не. Със (r-1) (c-1) степени на свобода

Където Oi е наблюдаваната честота, r е броят на редовете, c е броят на колоните и Ei е очакваната честота

Забележка: - Две случайни променливи се наричат ​​независими, ако разпределението на вероятностите на една променлива не се влияе от другата.

Използва

Тестът за независимост е подходящ за следните ситуации:

• Има една категорична променлива.
• Има две категорични променливи и ще трябва да определите връзката между тях.
• Има кръстосани таблици и трябва да се намери връзката между две категориални променливи.
• Съществуват количествено измерими променливи (например отговори на въпроси като, избират ли служителите в различни възрастови групи различни видове здравни планове?)

Как да направя теста Chi-Square в Excel? (с пример)

Управителят на ресторант иска да намери връзката между удовлетвореността на клиентите и заплатите на хората, които чакат маси. В това, ние ще създадем хипотезата за тестване на Chi-Square

• Тя взема произволна извадка от 100 клиенти, които питат дали услугата е била отлична, добра или лоша.
• След това тя категоризира заплатите на чакащите хора като ниски, средни и високи.
• Да приемем, че нивото на значимост е 0,05. Тук H0 и H1 означават независимостта и зависимостта на качеството на услугата от заплатите на чакащите хора.
• H ₀ - качеството на услугата не зависи от заплатите на хората, които чакат масите.
• H ₁ - качеството на услугата зависи от заплатите на хората, които чакат масите.
• Нейните открития са показани в таблицата по-долу:

В това имаме 9 точки с данни, имаме 3 групи, всяка от които получи различно съобщение относно заплатата и резултатът е даден по-долу.

Сега ще преброим сумата на всички редове и колони. Ще направим това с помощта на формула, т.е. SUM. За да обобщим отличното в общата колона, ние написахме = SUM (B4: D4) и след това натиснете клавиша enter.

Това ще ни даде 26 . Ще изпълним същото с всички редове и колони.

За да изчислим степента на свобода (DF), използваме (r-1) (c-1)

DF = (3-1) (3-1) = 2 * 2 = 4

• Има 3 категории услуга и 3 категории заплата.
• Имаме 27 респонденти със средна заплата (долен ред, средна)
• Имаме 51 респонденти с добра услуга (последна колона, средна)

Сега трябва да изчислим очакваните честоти: -

Очакваните честоти могат да бъдат изчислени по формула: -

• За да изчислим за Отличен, ще използваме умножаване на сумата на Ниска с сумата на Отличен, разделена на N.

Да предположим, че трябва да изчислим за 1-ви ред и 1-ва колона (= B7 * E4 / B9 ) . Това ще даде очаквания брой клиенти, които са гласували Отлично обслужване за заплатите на хората, които чакат като ниски, т.е. 8,32 .

• E _{11 =} - (32 * 26) / 100 = 8,32 , E ₁₂ = 7,02 , E ₁₃ = 10,66
• Е ₂₁ = 16,32 , Е ₂₂ = 13,77 , Е ₂₃ = 20,91
• E ₃₁ = 7,36 , E ₃₂ = 6,21 , E ₃₃ = 9,41

По същия начин за всички трябва да направим същото и формулата се прилага в диаграмата по-долу.

Получаваме таблицата на очакваната честота, както е дадена по-долу: -

Забележка: - Да приемем, че нивото на значимост е 0,05. Тук H0 и H1 означават независимостта и зависимостта на качеството на услугата от заплатите на чакащите хора.

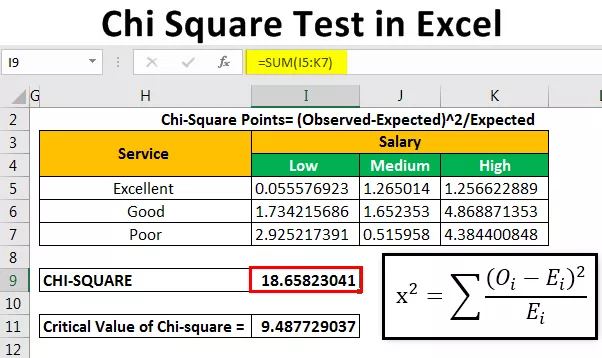
След изчисляване на очакваната честота, ние ще изчислим точките на хи-квадрат с помощта на формула.

Хи-квадрат точки = (Наблюдавано-очаквано) 2 / очаквано

За да изчислим първата точка, пишем = (B4-B14) 2 / B14.

Ще копираме и поставим формулата в други клетки, за да попълним автоматично стойността.

След това ще изчислим хи-стойността (Изчислена стойност), като добавим всички стойности, дадени над таблицата.

Чи-стойността получихме като 18.65823 .

За да изчислим критичната стойност за това, използваме таблица с критични стойности хи-квадрат, за да можем да използваме формулата, дадена по-долу.

Тази формула съдържа 2 параметъра CHISQ.INV.RT (вероятност, степен на свобода).

Вероятността е 0,05 и това е значителна стойност, която ще ни помогне да определим дали да приемем нулевата хипотеза (H ₀ ) или не.

Критичната стойност на хи-квадрат е 9,487729037.

Сега ще намерим стойността на хи-квадрат или (P-стойност) = CHITEST (действителен_диапазон, очакван_диапазон)

Обхват от = CHITEST (B4: D6, B14: D16) .

Както видяхме, стойността на хи-теста или P-стойността е = 0,00091723.

Изчислили сме всички стойности. Стойностите на хи-квадрат (Изчислена стойност) са значими само когато стойността му е еднаква или по-голяма от критичната стойност 9.48, т.е. критичната стойност (таблична стойност) трябва да е по-висока от 18.65, за да се приеме нулевата хипотеза (H ₀ ) .

Но тук Изчислена стойност > Таблична стойност

X ² (изчислено)> X ² (таблично)

18,65> 9,48

В този случай ще отхвърлим нулевата хипотеза (H ₀ ) и ще бъде приета алтернатива (H ₁ ) .

• Също така можем да използваме P-Value, за да предскажем същото, т.е. ако P-стойност <= α (значителна стойност 0,05), нулевата хипотеза ще бъде отхвърлена.
• Ако P-стойността> α , не отхвърляйте нулевата хипотеза .

Тук P-стойност (0,0009172) < α (0,05), отхвърлете H ₀ , приемете H ₁

От горния пример заключаваме, че качеството на услугата зависи от заплатите на чакащите.

Неща за запомняне

• Разглежда квадрата на стандартна нормална променлива.
• Оценява дали честотите, наблюдавани в различни категории, се различават значително от честотите, очаквани при определен набор от предположения.
• Определя доколко предполагаемото разпределение отговаря на данните.
• Използва непредвидени таблици (при пазарни проучвания тези таблици се наричат ​​кръстосани раздели).
• Той поддържа измервания на номинално ниво.