Формула за изчисляване на анюитетно плащане
Терминът „анюитет“ се отнася до поредицата периодични плащания, които трябва да бъдат получени или в началото на всеки период, или в края на периода в бъдеще. Формулата за анюитетно плащане и дължима рента се изчислява въз основа на PV на анюитет, ефективен лихвен процент и брой периоди.
Формулата, базирана на обикновен анюитет, се изчислява въз основа на PV на обикновен анюитет, ефективен лихвен процент и няколко периода.
Анюитет = r * PVA Обикновен / (1 - (1 + r) -n )където,
- PVA Ordinary = Сегашна стойност на обикновен анюитет
- r = ефективен лихвен процент
- n = Брой периоди
Математически уравнението за дължимата рента се представя като,
Рента = r * PVA дължимо / ((1 - (1 + r) -n ) * (1 + r))където,
- PVA Due = Сегашна стойност на дължима анюитетна вноска
- r = ефективен лихвен процент
- n = брой периоди

Как да изчислим анюитетно плащане? (Стъпка по стъпка)
Изчисляването на анюитетното плащане може да бъде получено чрез използване на PV на обикновената рента в следните стъпки:
- Стъпка 1 : Първо, определете PV на анюитета и потвърдете, че плащането ще бъде извършено в края на всеки период. Обозначава се с PVA Ordinary .
- Стъпка 2: След това определете лихвения процент въз основа на текущата възвръщаемост на пазара. След това ефективният лихвен процент се изчислява чрез разделяне на годишния лихвен процент на броя на периодичните плащания за една година и се обозначава с r. r = Годишен лихвен процент / Брой редовни плащания за една година
- Стъпка 3: След това определете броя на периодите, като умножите броя на периодичните плащания за една година и броя на годините, и той се обозначава с n. n = брой редовни плащания за една година * Брой години
- Стъпка 4: И накрая, анюитетното плащане въз основа на PV на обикновен анюитет се изчислява въз основа на PV на обикновен анюитет (стъпка 1), ефективен лихвен процент (стъпка 2) и някои периоди (стъпка 3), както е показано по-горе.
Изчисляването на анюитетното плащане може да се изведе и чрез използване на PV на анюитет, дължим в следните стъпки:
- Стъпка 1: Първо, определете PV на анюитета и потвърдете, че плащането ще бъде извършено в началото на всеки период. Обозначава се с PVA Due .
- Стъпка 2: След това определете лихвения процент въз основа на текущата възвръщаемост на пазара. След това ефективният лихвен процент се изчислява чрез разделяне на годишния лихвен процент на броя на периодичните плащания за една година и се обозначава с r. r = Годишен лихвен процент / Брой редовни плащания за една година
- Стъпка 3: След това определете броя на периодите, като умножите броя на периодичните плащания за една година и броя на годините, и той се обозначава с n. n = брой редовни плащания за една година * Брой години
- Стъпка 4: Накрая, анюитетното плащане въз основа на PV на анюитет се изчислява въз основа на PV на анюитет (стъпка 1), ефективен лихвен процент (стъпка 2) и няколко периода (стъпка 3), както е показано по-горе.
Примери
Пример # 1
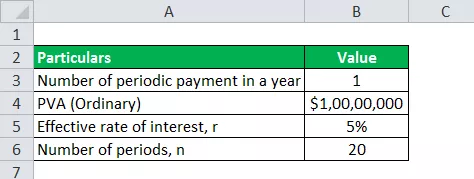
Нека вземем примера с Дейвид, който спечели лотария на стойност 10 000 000 долара. Той е избрал анюитетно плащане в края на всяка година за следващите 20 години като опция за изплащане. Определете сумата, която ще бъде платена на Дейвид като анюитетно плащане, ако постоянният лихвен процент на пазара е 5%.
По-долу са дадени данните, използвани за изчисляване на анюитетни плащания.
PVA Ordinary = $ 10,000,000 (от анюитета, който се изплаща в края на всяка година)
Следователно изчисляването на анюитетното плащане може да се направи, както следва -
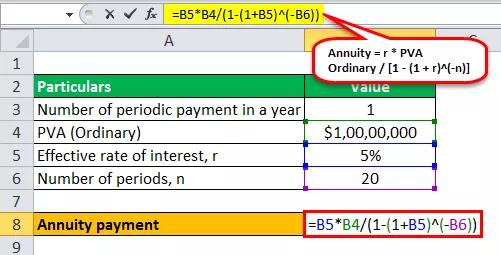
- Рента = 5% * 10 000 000 $ / (1 - (1 + 5%) -20 )
Изчисляването на анюитетно плащане ще бъде -

- Рента = 802 425,87 $ ~ 802 426 $
Следователно Дейвид ще плаща анюитетни плащания от $ 802 426 за следващите 20 години в случай на обикновен анюитет.
Пример # 2
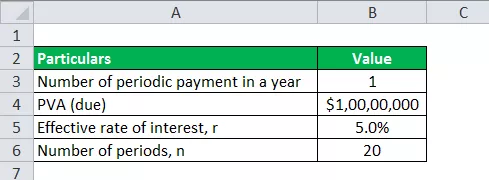
Нека вземем горния пример на Дейвид и да определим анюитетното плащане, ако е платено в началото на всяка година, при всички останали условия едни и същи.
Ще използваме същите данни като горния пример за изчисляване на анюитетни плащания.
Следователно изчисляването на анюитетното плащане може да се направи, както следва -
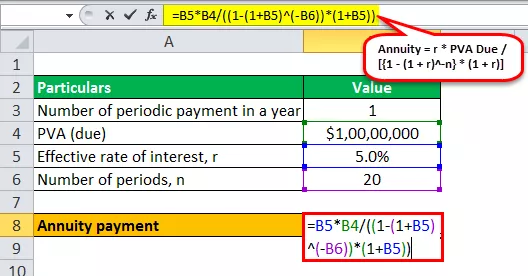
- Рента = r * PVA дължимо / ((1 - (1 + r) -n ) * (1 + r))
- Рента = 5% * 10 000 000 $ / ((1 - (1 + 5%) -20 ) * (1 + 5%))
Изчисляването на анюитетно плащане ще бъде -
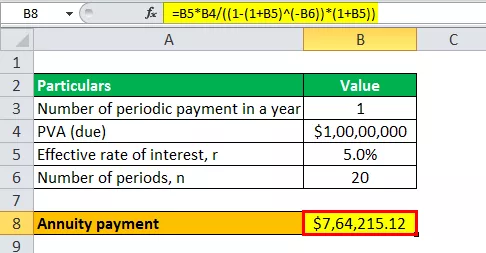
- Анюитет = $ 764 215,12 ~ $ 764 215
Следователно Дейвид ще плаща анюитетни плащания в размер на 764 215 долара за следващите 20 години в случай на дължима рента.
Анюитетен калкулатор
Можете да използвате следния анюитетен калкулатор.
| PVA Обикновен | |
| r | |
| н | |
| Формула за анюитет = | |
| Формула за анюитет = | r * |
|
||||||||
| 0 * |
|
Уместност и употреба
Анюитетното плащане е едно от приложенията на стойността на парите във времето, което допълнително се посочва от разликата между анюитетните плащания въз основа на обикновената рента и дължимата рента. По-ниското анюитетно плащане за анюитет е, че парите се получават в началото на всеки период. Смята се, че средствата ще бъдат инвестирани на пазара и лихвите ще бъдат спечелени през този период.
Уравнението за анюитетно плащане намира приложение при изчисляването на анюитетни доходи, амортизирани заеми, изплащания на лотарии, структурирани сетълменти и всеки друг вид фиксирани периодични плащания.