Какво е продължителността на Macaulay?
Продължителност на Macaulay е продължителността на времето, необходимо на инвеститора да възстанови инвестираните си пари в облигацията чрез купони и изплащане на главница. Този период от време е среднопретеглената стойност за периода, през който инвеститорът трябва да остане инвестиран в ценната книга, за да може настоящата стойност на паричните потоци от инвестицията да съответства на сумата, платена за облигацията.
Продължителността на Macaulay е много важен фактор, който трябва да имате предвид, преди да купите дългови инструменти. Това може значително да помогне на инвеститорите да избират измежду различни набори от налични ценни книжа с фиксиран доход на пазара. Както всички знаем, цените на облигациите са обратно свързани с лихвените проценти. Инвеститорите получават добра представа по отношение на това коя облигация да купят, по-дългосрочна или по-краткосрочна, ако знаят продължителността, която различните купонни облигации предлагат, заедно с прогнозната структура на лихвения процент.
Формула за продължителност на Маколи
Може да се изчисли, като се използва формулата по-долу,
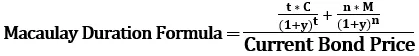

Където,
- t = период от време
- C = плащане с купон
- y = добив
- n = брой периоди
- M = падеж
- Текуща цена на облигациите = настоящата стойност на паричните потоци
Изчисляване на продължителността на Маколи с пример
Нека да видим пример за продължителността на Маколи, за да го разберем по-добре.
Облигацията на стойност 1000 щатски долара заплаща 8% купон и падежа в рамките на четири години. Купонната ставка е 8% годишно При полугодишно плащане. Можем да очакваме да възникнат следните парични потоци.
- 6 месеца: $ 40
- 1 година: $ 40
- 1,5 години: $ 40
- 2 години: $ 40
- години: $ 40
- 3 години: $ 40
- 3,5 години: 40 долара
- 4 години: 1040 долара
Изчислете продължителността на Маколи
Решение:
С горната информация можем да изчислим дисконтиращия фактор. Можем да използваме следната полугодишна формула за лихва, за да извлечем дисконтовия фактор. 1 / (1 + r) n, където r е процентът на купона, а n е броят на периодите, които се утежават.
Фактор на отстъпката
Изчисляването на дисконтовите фактори за 6 месеца ще бъде -

Фактори за отстъпка за 6 месеца = 1 / (1 + 8% / 2)
Фактори за отстъпка = 0,9615
По същия начин можем да направим изчисляването на дисконтовия коефициент за години 1 до 4.

Сегашна стойност на паричния поток
Настоящата стойност на паричния поток за 6 месеца ще бъде -

Сега, за да получим настоящата стойност на паричните потоци, трябва да умножим всеки период паричен поток със съответния му дисконтов фактор.
Настояща стойност на паричния поток за 6 месеца: 1 x 40 $ x 0,9615
Сегашна стойност на паричния поток = $ 38,46
По същия начин можем да направим изчисляването на настоящата стойност на паричния поток за година 1 до 4.

Продължителност на Маколи
Изчисляването на продължителността на Маколи ще бъде -

- Текуща цена на облигациите = PV на всички парични потоци 6 079,34
- Продължителност на Macaulay = $ 6 079,34 / $ 1000 = 6,07934
Можете да се обърнете към дадения шаблон на Excel по-горе за подробно изчисляване на продължителността на Маколи.
Предимства на използването на продължителността
Продължителността играе важна роля, за да помогне на инвеститорите да разберат рисковия фактор за наличната гаранция с фиксиран доход. Точно както как се измерва рискът в акции чрез отклонение от средната стойност или просто чрез извеждане на бета на ценната книга, рискът в инструментите с фиксиран доход се оценява стриктно от продължителността на инструмента на Маколи.
Разбирането и сравняването на продължителността на инструментите на Macaulay може да изиграе дълъг път при избора на подходящото за вашия портфейл с фиксиран доход.
Неуспехи при използването на продължителността
Продължителността е добро приближение на ценовите промени за облигация без опция, но е добра само за малки промени в лихвените проценти. Тъй като промените в лихвените проценти стават по-големи, кривината на връзката цена-доходност на облигациите става по-важна. С други думи, линейната оценка на ценовите промени, като продължителността, ще съдържа грешки.
Всъщност връзката между цената на облигациите и доходността не е линейна, а изпъкнала. Тази изпъкналост показва, че разликата между действителните и прогнозните цени се увеличава с увеличаване на доходността. Тоест, разширяващата се грешка в прогнозната цена се дължи на кривината на действителната ценова пътека. Това е известно като степента на изпъкналост.
Долна линия
Знанията за продължителността на Маколи са от първостепенно значение за определяне на бъдещата възвръщаемост от инструментите с фиксиран доход. Поради това е много препоръчително за инвеститорите, особено за инвеститорите, които не са склонни към риск, да оценят и сравнят продължителността, предлагана от различните облигации, за да постигнат минимален дисперсионен микс и да получат максимална възвръщаемост с възможно най-малък риск. Също така, факторът на лихвения процент трябва да се има предвид преди вземането на решение за покупка.





