Сложно определение
Смесването е методът за изчисляване на лихвения процент, който на практика представлява лихва върху лихва, при която лихвата се изчислява върху инвестицията / първоначалната главница плюс спечелените лихви и други реинвестиции, с други думи спечелените лихви се натрупват до основната сума в зависимост от периода на депозит или заем това може да бъде месечно, тримесечно или годишно
Нека се опитаме да разберем какво е съставянето и как работи чрез някои основни примери
Топ 4 примера за сила на комбиниране
Пример # 1
Шейн и Марк решиха да инвестират 1 000 000 долара, но Шейн реши да инвестира с обикновени лихви, докато Марк инвестира в сложни лихви в продължение на десет години при 10% лихва. Нека видим какво се случва след десет години.
Решение:
И така, изчисляването на инвестицията на Шейн ще бъде -

Обща сума на печалбата = $ 200 000
С обикновена лихва, Шейн ще получи $ 2 000 000 след 10 години.
Изчисляването на марковата инвестиция ще бъде -

Обща сума на печалбата = $ 2,59,374
Със сложната лихва инвестиционните стойности на Марк ще нараснат до 2 599 374 долара.
Сега Шейн реши да инвестира чрез комбинирани методи като Марк и двамата инвестираха 2,00 000 долара при ставка от 15%.
Изчисляването на инвестицията на Шейн ще бъде -

Обща сума на печалбата = $ 8,09,111.55
Шейн остава инвестиран в продължение на 10 години и получава окончателната сума от $ 8,09,111.55 в размер на 15%.
Изчисляването на марковата инвестиция ще бъде -

Обща сума на печалбата = $ 65,83,790.52
Въпреки това, Марк е търпение дългосрочни инвеститори и остава инвестиран в продължение на 25 години, а инвестиционната му стойност нараства до $ 65,83,790.52
Горният пример показва силата на смесването. Колкото по-дълъг е инвестиционният хоризонт, толкова по-голям е експоненциалният растеж.
Пример # 2 (седмично)
Саймън има спестявания от $ 7500 и за колежанския фонд на сина си, който ще посещава колежа след 15 години, той реши да инвестира в американски спестовни облигации. Целта на Саймън е да спести 20 000 долара, а годишният процент за американските облигации за спестяване е 6%. Каква е бъдещата стойност на Simon Money след 15 години?
Решение:
Като се има предвид,
- Главница = $ 7500
- Ставка = 6% или 0,06
- Период = 15 години.
- Колко пъти е съставен за една година n = 52 седмици
- Бъдеща стойност =?
И така, изчисляването на бъдещата стойност ще бъде -

Формулата за седмично смесване е както по-долу.
F = P (1 + r / n) n * t- F = 7500 $ (1 + 0,06 / 52) 52 * 15
- F = $ 7500 (1 + 0,001153846) 780
- F = 18 437,45 долара
Така че от горното изчисление става ясно, че целта на Саймън да спести $ 20,00 няма да бъде постигната с горните методи, но е по-близо до това.
Метод на непрекъснато съединение
Сега нека опитаме горния пример с формула за непрекъснато съединение.
И така, изчисляването на бъдещата стойност ще бъде -

- F = $ 7500e 0,06 * 15
- F = $ 7500e 0,9
- Бъдеща стойност (F) = 18 447,02 долара
Сега дори и с Continuous Compounding, целта на Саймън да спести 20 000 долара за колежански фонд на сина си няма да бъде постигната.
Нека видим с месечната формула, че колко пари са били необходими на Саймън, за да постигне целта си да спести $ 20 000 за 15 години при ГПР от 6%?
И така, изчисляването на бъдещата стойност ще бъде -
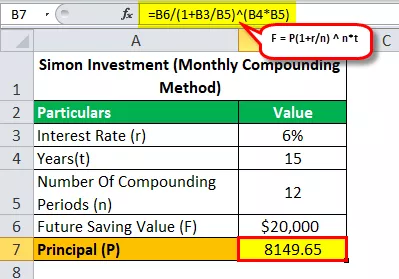
- 20 000 долара = P (1 + 0,06 / 12) 12 * 15
- P = $ 20 000 / (1 + 0,06 / 12) 12 * 15
- Главница (P) = 8149,65
Така че, като решим горното уравнение, ще получим отговор, който е $ 8,149.65 (сума, която Саймън трябва да инвестира, за да постигне целта си да спести $ 20 000 за 15 години).
Пример # 3 (Ефективен годишен добив)
Нека да кажем, че XYZ лимитираната банка дава 10% годишно на възрастни граждани за фиксиран депозит и тук приемаме, че банковите лихви се затрудняват на тримесечие като всички други банки. Изчислете ефективния годишен добив за 5, 7 и 10 години.
Решение:
Годишен добив за 5 години:
- t = 5 години
- n = 4 (на тримесечие)
- I = 10% годишно
Така че A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 за 5 години
Ефективна лихва = 0.6386 / 5
Ефективен I = 12,772% на годишна база
Годишен добив за 7 години:
- t = 7 години
- n = 4 (на тримесечие)
- I = 10% годишно
Така че A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1.9965
- I = 1.9965 за 7 години
- Ефективен I = 0,9965 / 7
Ефективен I = 14,236% на годишна база
Годишен добив за 10 години:
- t = 10 години
- n = 4 (на тримесечие)
- I = 10% годишно
Така че A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- А = 2,685
- I = 1,685 за 10 години
- Ефективен I = 1.685 / 10
Ефективен I = 16,85% на годишна база
Пример # 4 - (Ренти: бъдеща стойност)
1000 долара се инвестират на всеки 3 месеца при 4.8% годишно, комбинирани на тримесечие. Колко ще струва анюитетът след 10 години?
Решение:
Така че, когато казваме колко ще струва анюитетът след 10 години, тук трябва да намерим бъдеща стойност и това е важно, защото винаги, когато има пример за анюитети, трябва да видим какво трябва да разберем.
И така, формулата на бъдещата стойност е
FV на анюитет = P ((1+ r) n - 1 / r)- P = Периодично плащане
- r = ставка за период
- n = Брой периоди
Така че формулата на бъдещата стойност е
- Така че тук P = $ 1000
- r = 4,8% на годишна база или 0,048
- r (на тримесечие) = 0,048 / 4
- r (на тримесечие) = 0,012
- n = 10 години
- n (Брой пъти ще се прилага смесване) = 10 × 4 = 40
И така, изчисляването на FV на анюитета ще бъде -

Така че сега FV = $ 1000 (1 + 0,012) 40 -1 / 0,012)
Така че чрез решаване на горното уравнение ще получите FV от $ 50,955.30
И така, колко ще бъде анюитетът след 10 години и отговорът е $ 50,955.30
Освен това можем да разберем и от горния пример, че колко лихва се печели за 10 години.
Тъй като се инвестират 40 пъти по $ 1000, това е обща инвестиция (40 × $ 1000 = $ 40 000).
Така лихва = бъдеща стойност - обща инвестиция
- Лихва = $ 50 955,30 - $ 40 000
- Лихва = 10 955,30 долара
Така че тук е важно да се разбере, че в Анюитетите инвеститорите могат да спечелят голям интерес. В горните конкретни примери депозит от $ 40 000 дава в замяна обща лихва от $ 10 955,30.
Забележка: Можете да изтеглите предоставения по-горе шаблон на Excel за подробно изчисление.








