Какво представлява коефициентът на корелация?
Коефициентът на корелация се използва, за да се определи колко силна е връзката между две променливи и неговите стойности могат да варират от -1,0 до 1,0, където -1,0 представлява отрицателна корелация и +1,0 представлява положителна връзка. Той разглежда относителните движения на променливите и след това определя дали има някаква връзка между тях.
Формула на коефициента на корелация
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Където
- r = коефициент на корелация
- n = брой наблюдения
- x = 1- ва променлива в контекста
- y = 2- ра променлива
Обяснение
Ако има някаква корелация или да кажем връзката между две променливи, тогава тя указва дали една от променливите се променя в стойността, тогава другата променлива също ще има тенденция да се променя в стойността, да речем в конкретна, която може да бъде или в същата, или в обратната посока. Частта на числителя в уравнението провежда тест и относителна сила на променливите, които се движат заедно, а знаменателната част на уравнението мащабира числителя чрез умножаване на разликите на променливите от квадратни променливи.
Примери
Пример # 1
Помислете за следните две променливи, x и y, от вас се изисква да изчислите коефициента на корелация.
По-долу са дадени данни за изчислението.

Решение:
Използвайки горното уравнение, можем да изчислим следното

Имаме всички стойности в горната таблица с n = 4.
Нека сега въведем стойностите за изчисляване на коефициента на корелация.

Следователно изчислението е както следва,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Коефициентът ще бъде -

Коефициент = 0.99932640
Пример # 2
Държава Х е развиваща се икономическа държава и тя иска да извърши независим анализ на решенията, взети от нейната централна банка по отношение на промените в лихвените проценти, дали те са повлияли на инфлацията и дали централната банка може да контролира същото.
След обобщението на лихвения процент и инфлацията, които преобладаваха средно в страната за тези години, са дадени по-долу.
По-долу са дадени данни за изчислението.

Президентът на страната се обърна към вас, за да проведете анализ и да представите презентация по същия въпрос на следващата среща. Използвайте корелация и определете дали централната банка е постигнала целта си или не.
Решение:
Използвайки обсъдената по-горе формула, можем да изчислим коефициента на корелация. Третиране на лихвения процент като една променлива, да речем x, и третиране на инфлацията като друга променлива като y.

Имаме всички стойности в горната таблица с n = 6.
Нека сега въведем стойностите за изчисляване на коефициента на корелация.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Корелацията ще бъде -

Корелация = -0,92
Анализ: Изглежда, че корелацията между лихвения процент и инфлацията е отрицателна, което изглежда е правилната връзка. С нарастването на лихвения процент инфлацията намалява, което означава, че те са склонни да се движат в обратна посока една от друга и от горния резултат изглежда, че централната банка е успяла да приложи решението, свързано с лихвената политика.
Пример # 3
Лабораторията на ABC провежда изследвания на височината и възрастта и иска да разбере дали има някаква връзка между тях. Те са събрали извадка от 1000 души за всяка от категориите и са намерили средна височина в тази група.
По-долу са дадени данни за изчисляване на коефициента на корелация.

От вас се изисква да изчислите коефициента на корелация и да стигнете до заключението, че ако съществува някаква връзка.
Решение:
Третиране на възрастта като една променлива, да речем x, и третиране на височината (в cms) като друга променлива като y.

Имаме всички стойности в горната таблица с n = 6.
Нека сега въведем стойностите за изчисляване на коефициента на корелация.

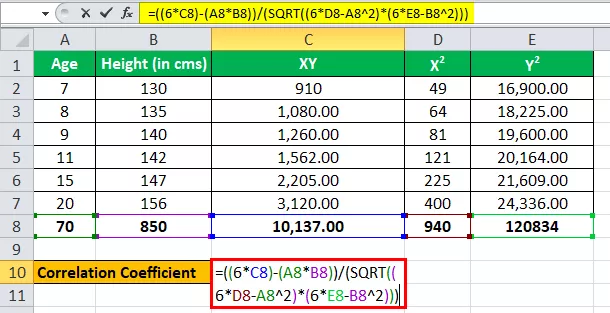
r = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1 322,00 / 1 361,23
Корелацията ще бъде -

Корелация = 0.971177099
Уместност и употреба
Той се използва в статистиката главно за анализ на силата на връзката между разглежданите променливи и освен това измерва дали има някаква линейна връзка между дадените набори от данни и колко добре те могат да бъдат свързани. Една от често срещаните мерки, които се използват за корелация, е коефициентът на корелация на Пиърсън.
Ако променлива променя стойността и заедно с тази друга променлива променя стойността, тогава разбирането на тази връзка е критично, тъй като може да се използва стойността на първата променлива, за да се предвиди промяната в стойността на последната променлива. Днес една корелация има многобройни употреби в тази модерна епоха, както се използва във финансовата индустрия, научните изследвания и къде ли още не. Но е важно да се знае, че корелацията има три основни типа взаимоотношения. Първият е положителна връзка, която гласи, ако има промяна в стойността на променлива, тогава ще има промяна в свързаната променлива в същата посока. По същия начин, ако има отрицателна връзка, тогава свързаната променлива ще се държи в обратна посока. Също така, ако няма корелация, тогава r ще означава нулева стойност.Вижте изображенията по-долу, за да разберете по-добре концепцията.









